Celine Ingrid Gomes dos Santos – Matemática, UFCG
celineingridgomess@hotmail.com
Programa de Educação Tutorial (PET) – Matemática e Estatística
A Álgebra Linear é um ramo da Matemática que estuda as propriedades dos espaços vetoriais e as transformações lineares. Essa área é fundamental para a resolução de problemas que envolvem sistemas lineares e Geometria Analítica.
Dentre as vastas aplicações aos diversos campos da ciência, destacamos que a Álgebra linear desempenha um papel importante na teoria de jogos. Por meio dela, é possível modelar e analisar as estratégias dos jogadores utilizando vetores, por exemplo. Além disso, cabe destacar, ainda, que “situações de conflito, ou qualquer outra forma de interação podem ser consideradas como jogos e as pessoas que participam desses eventos são chamados de jogadores.” (SOARES, 2007, p. 9)
Os resultados, definições e exemplos contextualizados que serão apresentados aqui foram todos retirados das referências [1] e [2].
Vamos considerar um jogo genérico de parque de diversões em que dois oponentes, os quais chamaremos de L e C, escolhem estratégias distintas. Cada jogador possui uma roda estacionária com um ponteiro móvel fixado em seu centro, semelhante a um relógio.
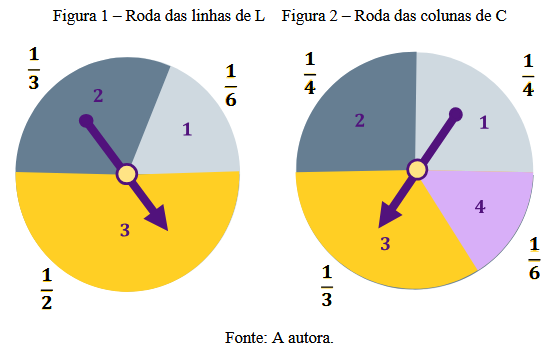
Denominaremos a roda dos jogadores L e C como roda das linhas e roda das colunas, respectivamente. Desse modo, é perceptível que a roda das linhas é dividida em três setores, enquanto a das colunas é dividida em quatro.
Para jogar, cada um dos participantes gira o ponteiro de sua roda, até que ele pare em um dos setores aleatoriamente. O número do setor em que a roda parar é chamado de movimento do jogador. Assim, vemos que L tem três possíveis movimentos e C possui quatro. E, ainda, é importante destacar que os jogadores não têm controle dos seus movimentos, ou seja, o movimento é feito aleatoriamente, de acordo com o resultado da roleta.
De acordo com o movimento feito por cada jogador, o participante C faz um pagamento em dinheiro para L, conforme ilustra a tabela a seguir. Por exemplo, se o participante L fizer o movimento 1 e o participante C fizer o movimento 2, então C fará um pagamento de R$ 5,00 para L. Além disso, as entradas negativas da tabela indicam que o jogador C deve fazer um pagamento negativo ao seu oponente. Em outras palavras, L fará um pagamento positivo a C.
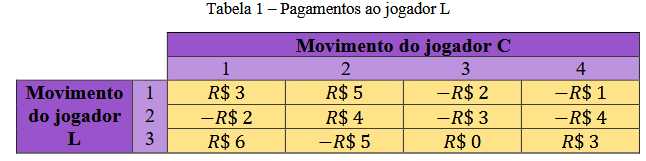
Perceba que a cada vez que é jogado, o ganho positivo de L é igual ao ganho
negativo de C, e vice-versa. Devido a isso, esse tipo de jogo é chamado de jogo de matriz
de duas pessoas com soma zero, uma vez que, ao somar os respectivos ganhos citados, o
resultado é igual a zero.
Observe que a probabilidade do jogador fazer um determinado movimento é dado
pela razão da área do setor correspondente pela área da roleta completa. Por exemplo, a
probabilidade do jogador L fazer a jogada 1 é de $ \frac{1}{6} $, e a probabilidade do jogador C fazer
o movimento 3 é de $ \frac{1}{3} $.
De modo geral, seja $ m $ o número de possíveis movimentos do jogador L e $n $ o de C. Em um lance qualquer desse jogo, cada um dos jogadores faz um de seus possíveis movimentos e, assim, é feita uma compensação do jogador C para o L. Essa compensação pode ser em qualquer espécie de bem ao qual possamos atribuir um valor numérico.
Para $ 𝑖 = 1,\cdots, 𝑚$ e $𝑗 = 1,\cdots, 𝑛$, denote $ a_{ij} $ a compensação do jogador C para o jogador L, se o jogador L faz o movimento $ 𝑖 $ e o jogador C faz o movimento $ 𝑗 $. Dessa forma, arranjamos essas $ mn $ compensações possíveis da forma mais natural: no formato de uma matriz $ m \times n$
\[ \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \]
a qual será chamada 𝑚𝑎𝑡𝑟𝑖𝑧 𝑑𝑒 𝑐𝑜𝑚𝑝𝑒𝑛𝑠𝑎çã𝑜.
