Ronaldo Costa da Silva – Estatística, UFCG
ronaldo.costa@estudante.ufcg.edu.br
Programa de Educação Tutorial (PET) – Matemática e Estatística
Eu sei que Poisson é peixe em francês, mas eu estava falando de Siméon Denis Poisson, esse matemático e físico Francês conhecido simplesmente por Poisson e da sua distribuição de probabilidade que leva seu nome.
Poisson nasceu em 21 de junho de 1781 em Pithiviers, França. Em 1798 entrou na École Polytechnique em Paris, como primeiro colocado de sua turma, onde teve como orientadores dois grandes e famosos matemáticos que são Joseph-Louis Lagrange e Pierre Simon Laplace. Com apenas 18 anos, Poisson já publicava os seus primeiros trabalhos sobre o método de eliminação de Étienne Bézout e sobre o número de integrais de uma equação em diferenças finitas.
Além das suas contribuições na matemática, Poisson contribuiu também em outras áreas como na eletricidade e magnetismo, óptica, estatística e probabilidade, mecânica, termodinâmica entre outras áreas. Além de suas muitas memórias, Poisson publicou uma série de tratados, a maioria dos quais pretendia fazer parte de uma grande obra sobre física matemática.
Sua principal contribuição foi dada na probabilidade com a famosa distribuição de Poisson que foi descoberta por Siméon Denis Poisson (1781–1840) e publicada, em 1838 no seu trabalho Recherches sur la probabilité des jugements en matières criminelles et matière civile (“Pesquisa sobre a probabilidade em julgamentos sobre matérias criminais e civis”). O trabalho focava em certas variáveis aleatórias, 𝑋, que contavam, entre outras coisas, o número de ocorrências discretas de um certo fenômeno durante um intervalo de tempo.

Uma distribuição de probabilidade é um modelo probabilístico que relaciona um certo valor em estudo com a sua probabilidade de ocorrência. Existem dois tipos básicos comumente estudados de distribuição de probabilidade, as contínuas onde a variável que está sendo medida pode tomar valores em uma escala contínua como, por exemplo, no caso de um conjunto com valores possíveis que é infinito e incontável, e as discretas quando a variável que está sendo medida só pode assumir certos valores em conjuntos contáveis (enumeráveis) como, por exemplo, os números inteiros, os números racionais e etc.
A distribuição de Poisson tem eficácia comprovada em vários estudos, podendo-se citar alguns exemplos, como o estudo do histórico de preenchimento de vagas no Supremo Tribunal dos Estados Unidos, e o estudo para prever o número de vagas que apareceriam no futuro. Essas vagas ocorreram por morte ou aposentadoria de ministros do STF. Historicamente, as proporções de vagas por morte e de vagas por aposentadoria têm sido aproximadamente iguais em número. Uma terceira causa possível de vaga, seria o impeachment de um juiz em exercício, que nunca ocorreu (WALLIS, 1936); (COLE, 2010). Foi bastante utilizada também como ferramenta em estudo prático de estatística para determinar o comportamento futuro do mercado de ações americano (DUNLAP; STUDSTILL, 2013), e muitos outros exemplos, como estimar número de aviões que chegam a um aeroporto no mês, ou carros que cruzam um determinado cruzamento, entre outros, onde os eventos e ocorrências são raros.
Dizemos que uma variável aleatória X tem distribuição de Poisson com parâmetro λ (λ > 0) se sua função de probabilidade for dada por
[P(X = k) = \frac{\lambda^k}{k!} e^{-\lambda}, \quad \text{para } k = 0, 1, 2, \ldots]
Notação: X〜Poisson (λ) (lê-se “X tem distribuição de Poisson com parâmetro lambda”)
onde:
𝑃 é a função de probabilidade da variável X que pode assumir valores k = 0,1,2,…
λ corresponde ao número de ocorrências do fenômeno que se espera dentro de um determinado intervalo de tempo.
𝑒 é a constante de Euler cujo valor aproximado é 2,71828.
Esta distribuição é bastante interessante, pois pode ser utilizada em várias situações cotidianas como por exemplo:
1. Empresas de telemarketing utilizam esse modelo para determinar o número de chamadas telefônicas e quantificar o número de funcionários que irão contratar para suprir a demanda dos consumidores do serviço prestado.

2. Determinar o número de falhas de um computador num dia de operação, isto é importante para saber quantos computadores reservas a empresa vai adquirir, quantas peças reservas, quantos funcionários de TI e etc.

Fonte: <https://www.tuacarreira.com/quanto-ganha-um-analista-de-sistemas/>
3. Determinar a quantidade de carros que passam por um determinado ponto da estrada durante uma hora, isto é importante para saber quantos guichês vão ter nos pedágios e de quanto em quanto tempo a estrada precisa de reparos tendo em vista que um trecho com mais movimentos precisa de reparos com mais frequência.

Como já visualizamos diversos exemplos de como essa distribuição pode ser utilizada, vamos colocar a mão na massa e entender como o cálculo se dá de fato. Em uma empresa de telemarketing admitindo que um telefone recebe, em média, cinco chamadas por minuto e supondo que a distribuição de Poisson seja adequada nessa situação, vamos obter a probabilidade de que o telefone não receba chamadas durante um intervalo de um minuto.
Como em média o telefone recebe 5 chamadas por minuto considerando X o número de chamadas que chega num intervalo de 1 minuto, temos que X~Poisson(5), assim, a probabilidade do telefone receber 0 chamadas em 1 minuto é dada por:
[P(X = 0) = \frac{5^0e^{-5}}{0!} = e^{-5} = 0{,}0067]
Na figura 5 apresentamos os pares (𝑥, 𝑃(𝑋 = 𝑥)) para 𝑥 = 0, 1, 2,…,10
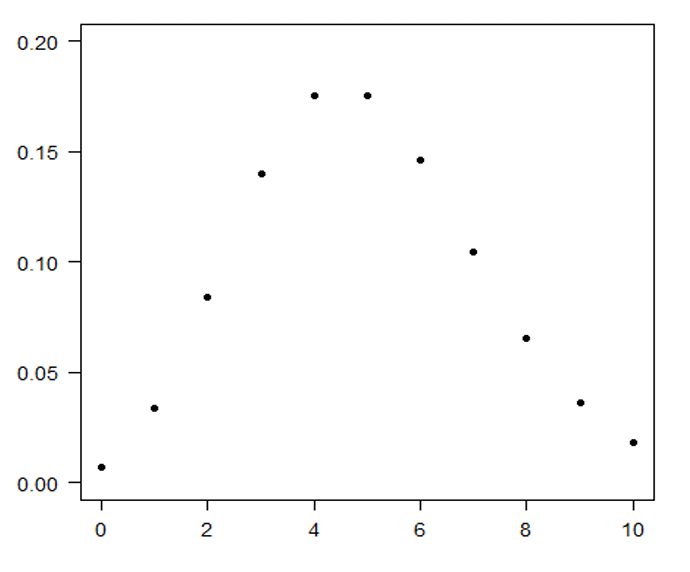
Fonte: Autoria própria.
Diante do exposto verificamos que esse modelo relativamente simples possui inúmeras aplicações em situações cotidianas, ao leitor que deseja aprofundar seus conhecimentos em James (2006) é possível estudar como é construído um processo de Poisson.
REFÊRENCIAS
- COLE, J. H. Updating a classic: “The Poisson distribution and the supreme court”. Teaching Statistic, v. 32, p. 78-80, 2010.
- DUNLAP, M.; STUDSTILL, S. A hands-on activity for teaching the Poisson Distribution using the stock market. Teaching Statistic, v. 33, n. 3, p. 88-92, 2013.
- WALLIS, W. The Poisson distribution and the Supreme Court. Journal of American Statistical Association, v. 31, n. 194, p. 376-380, 1936.
- SANTOS, M. R. S. Aplicação da Distribuição de Poisson para Determinação de Estoque Mínimo de Itens de MRO de Baixo Giro Aplicados em Manutenção de Ativos Industriais. Dissertação – Faculdade de Engenharia, Bauru, p. 52. 2015.
- MEYER, P. L. Probabilidade aplicações à estatística. 2. ed. Rio de Janeiro: Livros técnicos e científicos, 1983.
