Ísis Vieira Fernandes – Matemática, UFCG
isisvf11@gmail.com
Programa de Educação Tutorial (PET) – Matemática e Estatística
Ao falarmos sobre a matemática e as abelhas, a primeira coisa que nos vem à mente é o formato das colmeias. Sabemos que ao realizar um corte transversal na colmeia, obtemos um plano de hexágonos regulares, como mostra a Figura 1. Mas, porque as abelhas utilizam, exatamente, hexágonos e não triângulos, círculos ou, até mesmo, quadrados para construir as suas colmeias? Quais seriam as vantagens de utilizar os hexágonos e como é a real estrutura de cada alvéolo (também conhecido como favos)? Será que essas estruturas permitem um melhor aproveitamento do espaço e maior armazenamento de mel? É sobre esse assunto que vamos tratar no texto de hoje.

As abelhas constroem suas colmeias não apenas para guardar seu mel, mas também para o desenvolvimento e reprodução da sua própria espécie. Essas estruturas são formadas por vários alvéolos, construídos com cera, na forma de prisma reto hexagonal regular com um fundo não plano. Cada favo possui o mesmo tipo de fundo fechado por uma cobertura de três losangos, permitindo, assim, um encaixe entre os alvéolos.
Um dos primeiros estudiosos que se interessou pelas construções geométricas das abelhas e como são os favos de mel foi o geômetra (matemático especializado em geometria) grego Pappus de Alexandria (350 a.C. – 290 a.C.). Em seu ensaio denominado “A sagacidade das abelhas”, ele sugeriu que o padrão hexagonal repetitivo ao se realizar um corte transversal de um favo de mel era a opção arquitetônica que utilizava a menor quantidade de cera possível para construir suas separações. Essa hipótese ficou conhecida como “Conjectura do favo de mel” e só foi demonstrada em 1999, por Thomas Hales, da universidade de Michigan (MENEZES, 2017).
Para mostrar a veracidade dessa conjectura de forma simples, buscamos encontrar uma forma geométrica bidimensional que pudesse ser repetida indefinitivamente para cobrir uma área plana, de modo que o comprimento total dos perímetros das células fosse o menor possível para uma mesma área. Em (1), foi mostrado que só é possível preencher o plano com o mesmo polígono retangular “sem deixar espaço” usando triângulos equiláteros, quadrados e hexágonos regulares.
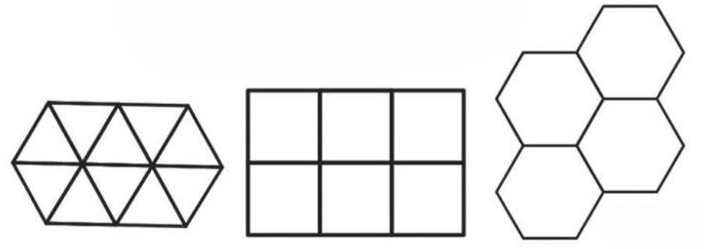
Fonte: MELO, 2014.
As abelhas poderiam utilizar qualquer uma dessas três formas, mas até mesmo as operárias não gostam de realizar trabalho desnecessário, então qual dessas três opções utilizaria um menor perímetro para que a menor quantidade de cera fosse utilizada? Agora, suponhamos que a área é igual para ambos os polígonos (𝐴) e vamos analisar qual deles tem menor perímetro. Denotando 𝐴 a área dos polígonos, 𝑙𝑛 o lado e 𝑃𝑛 o perímetro dos polígonos de 𝑛 lados, com 𝑛 = 3, 4 e 6. A área do triângulo equilátero é dada por
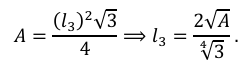
Assim, o seu perímetro é dado por
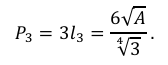
Para o quadrado, temos
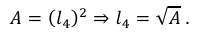
Logo,
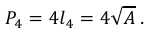
Por fim, a área do hexágono regular é dada por

Consequentemente
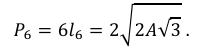
Como $\dfrac{6}{\sqrt[4]{3}} > 4 > 2\sqrt{2\sqrt{3}}$ (para demonstrar essa desigualdade, basta elevar os membros à quarta potência). Portanto, o que tem menor perímetro é o hexágono regular.
Quando analisamos os favos apenas em duas dimensões, vimos que as abelhas conseguem minimizar a quantidade de cera nos perímetros entre as estruturas. Mas, esses alvéolos devem ser tridimensionais para que ocorra o armazenamento de mel. Assim, as abelhas poderiam criar os alvéolos como prismas hexagonais, entretanto isso não permitiria um maior encaixe entre esses conjuntos de alvéolos denominados células.

Fonte: MENEZES, 2017
Apenas em 1619, o astrônomo e matemático Johannes Kepler (1571-1630) descreveu com precisão a formato do alvéolo como: prisma reto hexagonal regular cujo fundo é a união de três losangos congruentes determinando um triedro que possui seus ângulos diedras (ideia de ângulo estendido a figuras tridimensionais) de 120° (MENEZES, 2017). Dessa forma, “essas células encaixam-se perfeitamente nos fundos formando a colmeia que é a união de duas camadas desses alvéolos com aberturas hexagonais para entrada.” (RAFAEL & SALLUN, 2015).
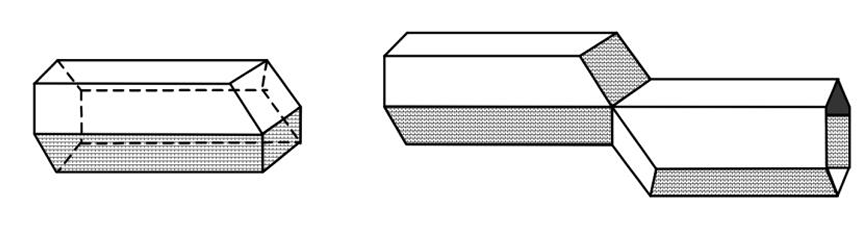
Fonte: SARAIVA,1999.
Entretanto, as abelhas não param por aí! Um biólogo e físico René-Antoine Ferhault de Réaumur (1683-1757), pensou: “Se as abelhas usam a forma hexagonal por economia de cera, elas devem usar o triedro com os três losangos no fundo também por economia”. E ele realmente acertou, quando propôs o seguinte problema ao seu amigo Johann Samuel König (1712-1757), como forma de comprovar sua hipótese:
Problema de Réaumur: Dado um prisma de base hexagonal, devemos fechá-lo em uma das extremidades com três losangos congruentes, colocados inclinadamente para obter o maior volume com um gasto mínimo de material. Quais são os ângulos internos dos losangos que satisfazem à condição?
Por mais que seu amigo König tenha conseguido resolver o problema, ele utilizou uma tabela de logaritmos pouco precisa. Então, um matemático escocês Colin Mac Laurin (1698-1746) melhorou os cálculos e obteve que os ângulos internos do losango são aproximadamente 109° 28′ e 70°32′. Dessa forma, obtemos um maior volume de fechamento, na qual o menor consumo de cera promove a maior capacidade de armazenamento de mel. Já em relação ao problema de Réaumur, deixamos como anexo um esboço de como resolvê-la, a partir dos conhecimentos de Cálculo Diferencial e Integral.
Portanto, notamos que as abelhas quando fabricam suas colmeias, utilizam alguns critérios geométricos que conduzem a um melhor aproveitamento do espaço e um maior armazenamento de mel. “Assim, nossas abelhas trabalhadoras, apesar de não resolverem problemas matemáticos, foram tão precisas quanto matemáticos do século XVIII”. (MELO, 2014).
ANEXO
Vamos expor um esboço de como resolver o problema de Réaumur. Essa será feita com base em Felipe Menezes (2017). Para mais detalhes consulte (2) ou (5).
Vamos considerar 𝜃 e 𝜓 = 180° − 𝜃 os ângulos internos de cada um dos losangos congruentes que compõem o ápice triédio, como mostra na figura abaixo:
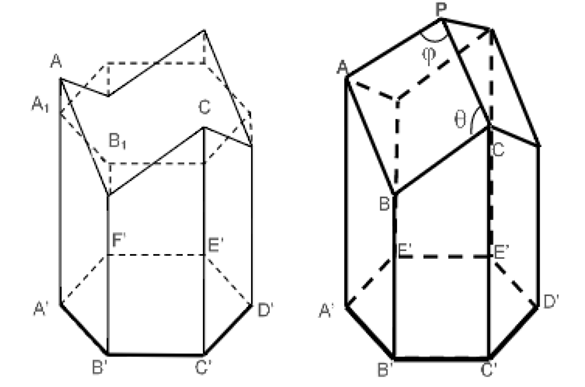
Fonte: VAIANO, A. Z; MÁRQUEZ, R. G.; ARAÚJO, J, 2015.
Logo, para achar esses ângulos, vamos encontrar uma expressão para a área total desse alvéolo em função de 𝜃 e, posteriormente, derivamos e igualamos a zero.
Para descobrir a área total, vamos determinar, primeiramente, cada área ($𝐴_𝐿$) dos losangos congruentes. Sendo 𝑙 a medida de cada lado do hexágono regular (𝐴′𝐵′𝐶′𝐸′𝐹′) da base e observando que a diagonal $\overline{AC}$ pode ser projetada ortogonalmente na base hexagonal gerando o segmento $\overline{A’C’}$ com mesma medida, temos que o triângulo 𝐴′𝐵′𝐶′ é isósceles e, aplicando a lei dos cossenos, obtemos:
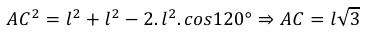
Assim, formamos o seguinte losango e podemos obter sua área
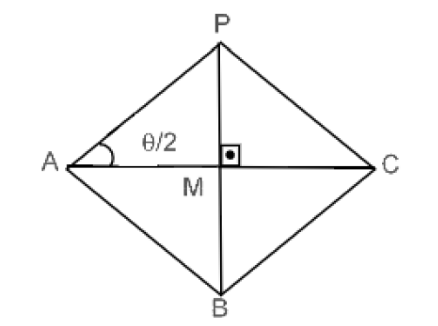
Fonte: VAIANO, A. Z; MÁRQUEZ, R. G.; ARAÚJO, J, 2015.
Note que
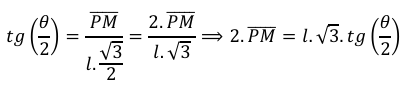
Assim, a área ($𝐴_𝐿$) de cada losango é
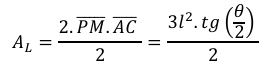
Agora, vamos determinar a área ($𝐴_𝑇$) de cada trapézio que compõe a lateral do alvéolo. Logo, vamos traçar um prolongamento do segmento $\overline{BB’}$ até $𝐵_1$, formando um triângulo $𝐴𝐵_1 𝐶$ que esteja contido no plano paralelo à base. Além disso, deduzimos que o triângulo $𝐵𝐵_1𝑀$ é retângulo em $𝐵_1$. Dessa forma, vamos determinar o segmento $\overline{BB_1}$ para encontrarmos a área de cada trapézio.
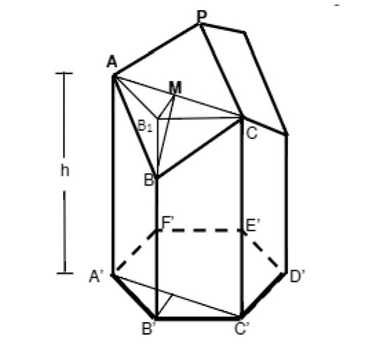
Fonte: VAIANO, A. Z; MÁRQUEZ, R. G.; ARAÚJO, J, 2015.
Vamos considerar ℎ a medida entre a base hexagonal e os vértices 𝐴 e 𝐶. Temos que, a medida do segmento $𝐵_𝑀$ equivale à medida de $𝑃_𝑀$ e a medida de $𝐵_1𝑀$ equivale à altura do triângulo 𝐴′𝐵′𝐶′. Daí, aplicando o Teorema de Pitágoras no triângulo $𝐵𝐵_1𝑀$, temos:
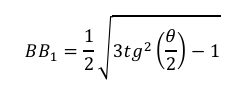
Logo, obtemos que a área $𝐴_𝑇$ de cada trapézio é:
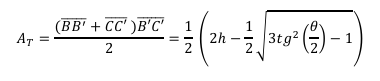
Portanto, a área total do alvéolo em função de 𝜃 é
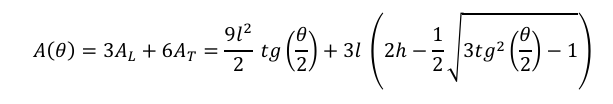
Por fim, para encontrar os ângulos 𝜃 e 𝜓 que minimiza a área total, basta derivar A(𝜃) em relação a 𝜃 e depois igualar a zero e, assim, encontramos que 𝜃 = 70,529° ≈ 70°32′ e como 𝜓 = 180° − 𝜃, encontramos que 𝜓 = 109°28′.
REFERÊNCIAS
- MELO, Helena Sousa. As abelhas trabalhadoras. Correio dos Açores, p. 16-16, 2014.
- MENEZES, Felipe R. A geometria das abelhas na construção de seus alvéolos. 2017. 73f. Dissertação (Mestrado Profissional em Matemática em Rede Nacional – PROFMAT) – Instituto de Matemática e Estatística – Universidade de Estado do Rio de Janeiro, Rio de Janeiro, 2017.
- RAFAEL, D. M; SALLUN, E. M. Oficina 3 – As abelhas conhecem geometria?, 2015. Disponível em: https://www.ime.usp.br/caem/anais_mostra_2015/arquivos_auxiliares/oficinas/Oficina03_Elvia_Debora.pdf. Acesso em: 05 mar. 2022.
- SARAIVA, J. C. A matemática das Abelhas. In: Revista Eureka! nº 6, p. 18-22. Rio de Janeiro: Sociedade Brasileira de Matemática SBM, 1999.
- VAIANO, A. Z; MÁRQUEZ, R. G; ARAÚJO, J. Abelhas africanizadas e construções geométricas. In: Congresso Scientiarum História VIII (In)certezas e (In)completudes, p. 5-9. Rio de Janeiro, 2015.
