Josefa Itailma da Rocha
itailma@mat.ufcg.edu.br
Tutora do grupo PET Matemática e Estatística -UFCG
O número 𝜋 é, sem dúvida, uma das constantes matemáticas mais conhecidas. Ele representa o valor constante que obtemos quando dividimos o comprimento de uma circunferência pelo seu diâmetro. O 𝜋 é um número irracional, ou seja, não pode ser escrito como o quociente de números inteiros e seu valor aproximado, com 4 casas decimais, é de 3,14156.
A primeira tentativa rigorosa de encontrar uma aproximação para o valor de 𝜋 deve-se a Arquimedes (matemático grego que viveu entre 287 a.C e 212 a.C.), que usou polígonos de 96 lados inscrito e circunscrito e encontrou que o valor de 𝜋 seria aproximadamente entre 3,1408 e 3,1429.
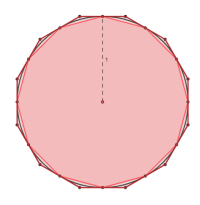
Fonte:https://www.gi2.pt/galerias/calculo-de-pi/
O matemático Ptolomeu, que viveu em Alexandria aproximadamente no século III d.C., conseguiu uma aproximação melhor que a obtida por Arquimedes, usando polígono de 720 lados inscrito numa circunferência. Seu valor encontrado foi de aproximadamente 3,1416. Ao longo dos anos, muitos matemáticos trabalharam no problema de encontrar uma aproximação para 𝜋. No século V, o matemático Tsu Ch’ung Chih conseguiu uma aproximação entre 3,1415926 e 3,1415927, como uma precisão de 6 casas decimais. Claramente, quanto maior o número de casas decimais, melhor é a precisão do valor encontrado. Hoje em dia, com o uso de supercomputadores, é possível aproximar o valor de 𝜋 com uma precisão de trilhões de casas decimais. A melhor aproximação do valor de 𝜋 foi obtida em agosto de 2021, pela Universidade de Ciências Aplicadas de Graubunden, na Suíça, e tem uma precisão de 62,8 trilhões de casas decimais.
Podemos encontrar o valor de 𝜋 usando o computador para desenhar círculos e dividindo o comprimento da circunferência pelo seu diâmetro. Por exemplo, usando o GeoGebra, podemos traçar um círculo qualquer. Na janela de Ferramentas, selecionando “Distância, comprimento” e clicando no círculo, será exibido o comprimento da circunferência. Depois disso, basta construir um diâmetro, usando o comando de reta e, da mesma forma feito para o círculo, calcular o seu comprimento. Na Figura 2, temos construído um círculo cujo comprimento da circunferência é 𝑐 = 18,77106 e o diâmetro é 𝑑 = 5,97501. Dividindo o comprimento da circunferência pelo diâmetro, obtemos
+
\frac{18.77106}{5.97501} = 3.1415947421
+
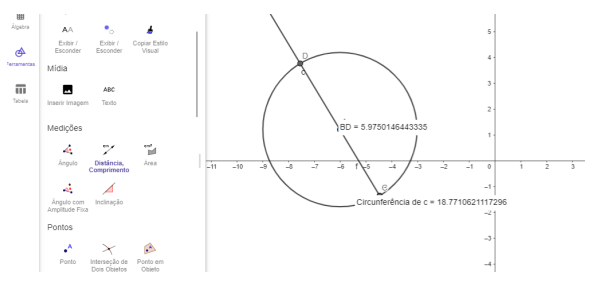
Fonte: Autora
Vejamos o que acontece quando tentamos repetir essa mesma experiência usando o Google Earth para desenhar círculos na superfície do planeta Terra. Na Figura 3, temos um círculo que engloba todo o Brasil desenhado no Google Earth. Pela janela de ferramentas conseguimos ver que o comprimento da circunferência é 𝑐 = 10.754,26 𝑘𝑚 e o raio é 𝑟 = 1.727,93 𝑘𝑚, assim o diâmetro da circunferência é 𝑑 = 3.455,86 𝑘𝑚. Dividindo o comprimento da circunferência pelo diâmetro obtemos
+
\frac{10{.}754{,}26}{3{.}455{,}86} = 3{,}1118911067,
+
que é menor do que o valor de 𝜋 que conhecemos.
Repetindo essa experiência com círculos cada vez maiores sobre a superfície da Terra, vemos que o quociente do comprimento da circunferência pelo diâmetro fica cada vez menor do que o valor de 𝜋.
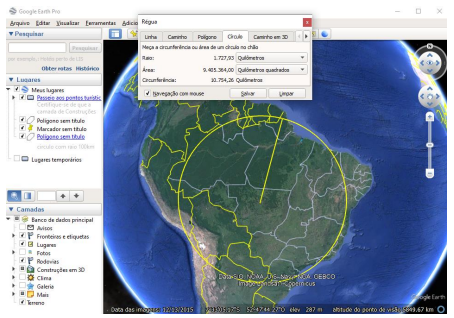
Fonte: Autora
Será que que o comprimento da circunferência pelo diâmetro não é constante e toda a matemática que estudamos está errada? É fato que esse resultado já foi provado pelos matemáticos gregos há muitos anos. Mas tem um pequeno detalhe. A prova dos gregos vale apenas para a Geometria Euclidiana, ou seja, para círculos no plano. E como todos sabemos, a Terra não é plana! Por isso, a geometria da Terra não obedece aos Teoremas obtidos na Geometria Euclidiana. Para entender um pouco mais sobre a Geometria da Terra, e porque nela a razão da circunferência pelo diâmetro não é constante e é sempre menor do que 𝜋, precisamos entender um pouco sobre as Geometrias não-Euclidianas, mas especificamente, sobre a Geometria Elíptica.
Euclides de Alexandria foi um matemático grego que viveu no século III a. C., e é considerado o pai da Geometria. Sua obra mais famosa é Os Elementos, livro que reúne todo o conhecimento da geometria de forma dedutiva, partindo de algumas definições, noções comuns e de apenas 5 postulados. Com esses elementos, Euclides conseguiu deduzir toda a geometria clássica através da Lógica matemática. Os cinco postulados da Geometria Euclidiana são:
- Pode-se traçar uma única reta ligando quaisquer dois pontos.
- Pode-se continuar (de uma maneira única) qualquer reta finita continuamente em uma reta.
- Pode-se traçar um círculo com qualquer centro e com qualquer raio.
- Todos os ângulos retos são iguais.
- Por um ponto fora de uma reta pode-se traçar uma única reta paralela à reta dada.
As Geometrias não-euclidianas surgem da negação do 5º postulado. Existem duas possibilidades para isso, que dão origem a Geometrias diferentes. A primeira delas seria:
“Por um ponto fora de uma reta, passam mais de uma reta paralela à reta dada.”
que dá origem a Geometria Hiperbólica, estudada principalmente pelo matemático russo Nikolai Lobachevsky.
A segunda maneira de negar o quinto postulado de Euclides é afirmando que:
“Por um ponto fora de uma reta, não passa nenhuma reta paralela à reta dada.”
que dá origem a Geometria elíptica, também conhecida como Geometria Riemanniana. A geometria esférica, que é a geometria da Terra, é um modelo mais simples da Geometria Elíptica, uma vez que toda esfera é uma elipse.
As geometrias não euclidianas possuem algumas diferenças da geometria euclidiana, além do 5º postulado de Euclides. Por exemplo, na Geometria Euclidiana, a soma dos ângulos internos de um triangulo é sempre igual a 180𝑜 . Na Geometria hiperbólica, a soma é menor que 180𝑜 , e na geometria elíptica é sempre maior.
Para entender o porquê de a razão da circunferência pelo diâmetro não ser igual a 𝜋 na geometria esférica, precisamos entender o conceito de Geodésicas, que são as curvas de menor distância na superfície que une dois pontos. No plano Euclidiano, sabemos a curva de menor distância que une dois pontos é uma reta, porém na Geometria da esfera, dois pontos não estão conectados por uma reta e sim por arcos de circunferências. A curva de menor distância que conecta dois pontos em uma esfera é um arco de grande círculo, que são círculos desenhados na superfície da esfera com o mesmo centro da esfera. Como quaisquer dois grandes círculos se encontram em pelo menos dois pontos, então não existem “reta paralelas” na esfera. Esse modelo é o mesmo usado na aviação. Os aviões não voam em linhas retas, senão eles teriam de passar por dentro da Terra ou eles sair da Terra. Na verdade, as órbitas dos aviões são definidas por arcos de grandes círculos que ligam o ponto de origem e o destino final da viagem.
Vamos imaginar agora que queremos desenhar um círculo na superfície da terra. Fixado o centro, considere um plano tangente a Terra que contêm esse ponto e desenhe um círculo no plano com esse centro. Projetando esse círculo para a superfície da Terra, vemos que na Terra ele terá um raio maior do que no plano, uma vez que a superfície da Terra se afasta do plano devido a sua curvatura.
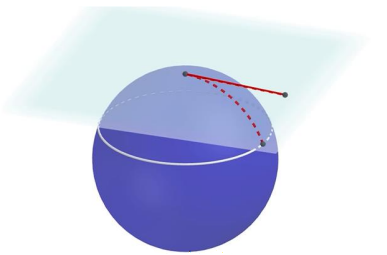
Fonte: https://www.youtube.com/watch?v=WVnzFOvxlg8&t=569s
Quanto maior o círculo, maior será a diferença entre o raio no plano e raio na superfície, apesar do comprimento da circunferência permanecer o mesmo. Isso ocorre, porque quanto maior o círculo, mais o raio irá se curvar na superfície da Terra, que fica cada vez mais distante do plano. Da mesma forma, se compararmos o círculo desenhado no plano e o círculo desenhado na esfera, para um mesmo raio, vamos notar que o círculo desenhado no plano é maior. Assim, o comprimento da circunferência no plano dividido pelo diâmetro do círculo é maior do que o comprimento da circunferência na esfera dividido pelo diâmetro, ou seja
+
\frac{\text{Comprimento da circunferência}}{\text{diâmetro}} = \pi
+
Quanto maior o círculo, maior será essa diferença. Como o nosso planeta é enorme, tem um raio de aproximadamente 6.371 km, então na prática a gente não consegue desenhar círculos grandes o suficiente na superfície a ponto de notar essa diferença. Os círculos que conseguimos são tão pequenos que essa razão é sempre muito próxima de 𝜋.
Referências
- NUNES, Daniel, canal Tem Ciência, Um jeito NOVO de PROVAR que a TERRA NÃO É PLANA (usando Pi), YouTube, 21 de março de 2022, Disponível em https://www.youtube.com/watch?v=WVnzFOvxlg8&t=569s
- Derivando a Matemática, Número Pi Historia e Aplicações, Disponível em https://www.ime.unicamp.br/~apmat/numero-pi/, acessado em 16 de maio de 2023.
