Celine Ingrid Gomes dos Santos – Matemática, UFCG
celineingridgomess@hotmail.com
Programa de Educação Tutorial (PET) – Matemática e Estatística
Ao estudarmos a Filosofia na Grécia, é comum ouvirmos falar das famigeradas artes liberais, dispostas nos grupos do trivium e quadrivium[1]. Nesse último, temos a presença da Música como disciplina essencial de ensino nas universidades desse período. No entanto, que relações podemos encontrar entre a Música e a Matemática? Existe algum elo entre as duas?
Conforme Wright (2009, p.8, tradução nossa) pontua,
Os conceitos musicais abordados incluem escalas diatônicas e cromáticas (padrão e fora do padrão), intervalos, ritmo, métrica, forma, melodia, acordes, progressões, equivalência de oitavas, harmônicos, timbre, formantes, temperamento igual, e métodos alternativos de ajuste. Os conceitos matemáticos abordados incluem números inteiros, números racionais e reais, relações de equivalência, transformações geométricas, grupos, anéis, aritmética modular, fatoração única, logaritmos, exponenciais e funções periódicas. Cada uma dessas noções entra em cena porque está envolvido de uma forma ou de outra com um ponto onde a matemática e a música convergem.
Segundo Simonato (2011), os povos da Antiguidade tiveram os sons organizados à sua maneira, de acordo com escalas e formas sonoras. Na China, por exemplo, houve o desenvolvimento das famosas escalas pentatônicas que, como sugere o nome, são uma sucessão de um conjunto de cinco notas ou tons. Já na Grécia, berço principal do progresso da teoria musical, temos o desenvolvimento dos tetracordes.
Consoante a isso, não há como falarmos de Música na Grécia sem citar o matemático, filósofo, astrônomo e músico Pitágoras de Samos (572 – 497), que tivera demasiada influência na descoberta das escalas musicais conhecidas atualmente. De acordo com Simonato (2011, p. 1),
[…] ao passar por uma oficina, ouviu o som de cinco martelos batendo numa bigorna. Admirado com o som agradável, e pensando inicialmente que a qualidade do som era proveniente da força das mãos, ele teria trocado os martelos, mas cada martelo conservava o som que lhe era próprio. Após ter tirado um que era desagradável, pesou os outros e constatou que o primeiro pesava doze, o segundo nove, o terceiro oito, o quarto seis, de uma unidade de peso desconhecida.
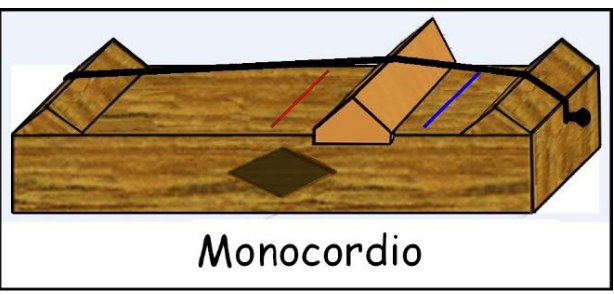
Ademais, também é atribuído ao músico grego Pitágoras a criação do monocórdio – instrumento composto por uma corda presa a uma caixa de madeira.
[1 Quatro artes liberais: Aritmética, Geometria, Música e Astronomia.]
Ainda segundo Simonato (2011), o monocórdio foi fundamental para a descoberta de que a altura de uma nota musical é diretamente proporcional ao comprimento da corda que a produz. Para tanto, Pitágoras notou que ao pressionar a corda em um ponto equidistante de suas duas extremidades, isto é, à metade de seu comprimento, e tocando-a, o som produzido era o mesmo que o da corda solta, no entanto, mais agudo. Musicalmente, conhecemos tal fenômeno por oitava. Analogamente, pressionou a corda em $[\frac{2}{3}]$ de seu comprimento e percebeu que o som gerado possuía relação com o som da corda solta. Nascera, assim, o som denominado por quinta. Um fato interessante é que o violão tem suas marcações de casas em seu braço determinadas a partir desses cálculos.
Ademais, Simonato (2011, p. 2) pontua que “os pitagóricos observaram que as notas diferenciadas por intervalos de oitava apresentavam certa semelhança, podendo ser definida como uma classe de equivalência[2]”. Dessa maneira, sejam $k$, $l$ inteiros quaisquer e $n$ um inteiro estritamente positivo. Diremos que $k$ é côngruo a $l$ módulo $n$ se $n|(k − l)$. Indicaremos que $k$ é côngruo a $l$ módulo $n$ pela notação:
+ k ≡ l \ (\text{mod} \ n). +
Essa relação de congruência é também de equivalência. Logo, cada classe de equivalência contém um inteiro do conjunto ${0, 1, 2 \cdots, n − 1}$ e, assim, existem $n$ classes de equivalência. O conjunto dessas classes é denotado por $\pi_n$.
Sob esse viés, Wright (2009, p. 31-32, tradução nossa) destaca que
O caso $n = 12$ tem um significado especial na música. […] Ao medir intervalos em semitons, o conjunto de intervalos é identificado com o conjunto $\pi$ dos inteiros, com um inteiro $k$ correspondente ao intervalo de $k$ semitons, para cima se $k$ for positivo, para baixo se $k$ for negativo. Com essa identificação, a equivalência módulo 12 nada mais é do que identificação de oitava: Dois intervalos de $k$ semitons e $l$ semitons são equivalentes módulo oitava se, e somente se, $k ≡ l \ (\text{mod} \ 12)$. Assim, cada classe de equivalência de intervalos contém um intervalo único de $r$ semitons com $0 ≤ r < 12$ (ou seja, um intervalo não negativo a menos de uma oitava), e este $r$ é obtido como o resto no Algoritmo da Divisão com $n = 12$.
[2 Conjunto composto por todos os elementos que se relacionam com um elemento x por meio de uma relação de equivalência.]
Em suma, além de todas as relações entre as duas ciências que mostramos aqui, podemos garantir que existem diversas outras aplicações da Matemática à Música. Algumas dessas são o grupo diedral de ordem 24 e o grupo das simetrias de um dodecágono, que modelam a escala cromática ou, ainda, as ondas sonoras, que podem ser estudadas utilizando séries de Fourier. Dessa forma, deixamos a cargo do leitor interessado a procura e estudo de temas tangentes aos que foram apresentados e que jamais percamos de vista que “quem canta reza duas vezes” (Santo Agostinho).
REFERÊNCIAS
[1] SIMONATO, Adriano Luís; DIAS, Maria Palmira Minholi. A Relação Matemática e Música. Revista Fafibe On-line, Bebedouro, v. 1, n. 1, p. 1-6, 2011.
[2] WRIGHT, David. Mathematics and Music. [S.l.]: American Mathematical Society, 2009.
