Ester Vanderlei Silva Avelino − Matemática, UFCG
ester.vanderlei@estudante.ufcg.edu.br
Programa de Educação Tutorial (PET) – Matemática e Estatística
No filme Homem-Aranha: Sem Volta Para Casa, 2021, Peter Parker confronta o Doutor Estranho na Dimensão Espelhada, e para superar os poderes místicos do mago, ele usa a força da matemática ao perceber que a dimensão mágica operava segundo as leis da geometria. Peter observou um padrão parecido com a Espiral de Arquimedes na forma em que os escombros da cidade de Nova Iorque estavam flutuando nessa dimensão. Então, o Homem-Aranha usa suas teias para desfazer a clássica forma da espiral e, no processo, prender o Doutor Estranho em seu centro. Entretanto, a Espiral de Arquimedes não se limita apenas para derrotar magos superpoderosos.
A Espiral de Arquimedes foi descoberta pelo matemático e astrônomo grego Canon de Samos (280 – 220 a.C.), entretanto ele morreu antes que pudesse estudar a fundo a nova descoberta. Quem fez isso foi o seu amigo Arquimedes de Siracusa (287–212 a.C.), na obra Sobre as Espirais, (VELOSO, 2017). Nessa obra, Arquimedes descreve a curva espiral da seguinte forma:
Se uma linha reta traçada em um plano gira com uma velocidade constante ao redor de uma extremidade que permanece fixa e retorna à posição de onde começou e se, no mesmo tempo em que a linha gira, um ponto desloca-se com uma velocidade constante ao longo da linha reta começando da extremidade que permanece fixa, o ponto vai descrever uma espiral no plano. (Archimedes, 2002).
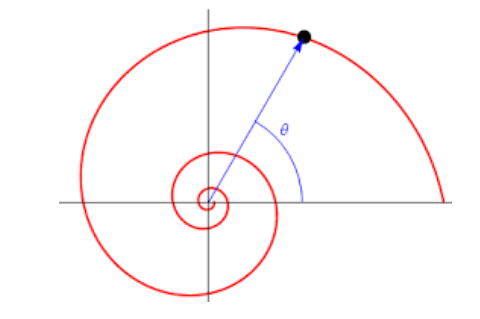
Figura 1: Espiral
Assim, a espiral de Arquimedes é uma figura geométrica determinada por um ponto movendo-se a velocidade constante sobre uma reta que gira sobre um ponto de origem fixo a velocidade angular constante. Essa espiral pode ser representada em coordenadas polares (r, θ), onde r é o raio e θ o ângulo, descrita pela seguinte equação:
𝑟 = 𝑎 + 𝑏𝜃, com a e b números reais (ALMEIDA, 2010).
A Espiral de Arquimedes tem infinitas aplicações no mundo real, sejam em áreas como a engenharia e arquitetura ou por sua presença em diferentes fenômenos na natureza. Vejamos alguns exemplos.
A indústria do setor de refrigeração doméstica utiliza os compressores de espiral, feitos de duas espirais de Arquimedes do mesmo tamanho intercaladas, que são usados para comprimir líquidos e gases (GOMES, 2006).
Figura 2: Processo de Compressão

Outra aplicação foi nos sulcos – que representam a vibração dos sons gravados – das primeiras gravações de disco de vinil, que por formarem uma espiral de Arquimedes, faziam os sulcos igualmente espaçados, maximizando o tempo de gravação que poderia acomodar-se na área do disco (SILVA, 2015)
Figura 3: Disco de Vinil
Ademais, um uso bastante interessante da espiral é no diagnóstico de enfermidades neurológicas. É um método em que se pede a um paciente que desenhe uma espiral de Arquimedes e através do traçado é possível extrair características que possibilitam a investigação do tremor cinético (ALMEIDA, 2010).
As espirais de Arquimedes também são usadas em microbiologia de alimentos para determinar a concentração bacteriana através de uma placa espiral. A técnica de plaqueamento em espiral é o método antigo e bastante conhecido e, para isso, utiliza-se um aparelho denominado Spiral Plater (Spiral Biotech, Inc, Bethesda, MD, EUA):
O instrumento succiona, através de uma bomba de vácuo, uma alíquota do produto em análise, adequadamente homogeneizado com um diluente, dispensando-a na superfície de uma placa com meio de cultura posicionada sobre uma plataforma giratória. A semeadura é feita automaticamente por urna cânula de teflon que se desloca do centro da placa para as suas bordas, à medida que a placa gira, formando uma espiral (espiral de Arquimedes). Forma-se um gradiente de concentração, que se inicia no centro e diminui à medida que se dirige para as bordas da placa O volume de liquido depositado em cada segmento da placa é conhecido. As placas inoculadas são incubadas e as colônias podem ser enumeradas colocando as placas em cima de um modelo no qual está impresso o desenho de urna placa subdividida em segmentos. A cada segmento corresponde um fator de multiplicação, relacionado com o volume de líquido nele depositado. Deve-se selecionar o segmento no qual a contagem de colônias é possível, multiplicando-se a contagem obtida pelo fator correspondente, obtendo-se assim o número de UFC por g ou por ml de produto. (FRANCO, 1994)
Na natureza, a espiral ocorre mais frequentemente do que qualquer outra curva. Bernoulli a chamava de “spira mirabilis” e a considerava notável pelas propriedades matemáticas que a torna única entre as curvas planas. Podemos observar na folha de uma espécie de samambaia (Figura 4), no girassol (Figura 5), em alguns redemoinhos de água e de ventos (Figura 6), no caracol (Figura 7) e na concha do Náutilo (Figura 8) a graciosidade dessa espiral na natureza.
Figura 4: Espécie rara de samambaia originaria da ilha do Havaí.
Figura 5: Girassol, planta originária da América do Norte.

Figura 6: Ciclone
Figura 7: Caracol, molusco terrestre.

Figura 8: Concha do Náutilo.

Outro local que podemos ver essa espiral é na Loxodromia. Esta é a linha que faz um ângulo constante com todos os meridianos, na superfície da Terra, ela não é o caminho mais curto entre dois pontos, mas é o trajeto mais simples e normalmente empregado em mapas rodoviários ou marítimos. Ao seguir a rota loxodrômica o navio não dará a volta ao mundo regressando ao ponto de partida. E é essa projeção estereográfica da linha loxodrômica no plano tangente ao polo que percebemos uma espiral (RESENDE, 2017).
Figura 9: Linha loxodrômica.
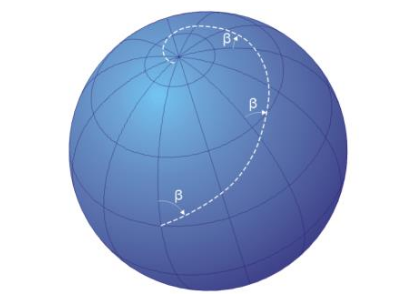
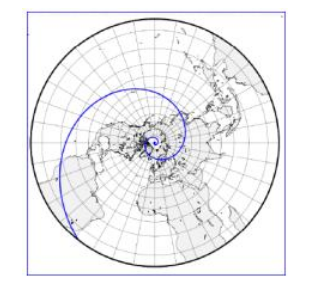
Figura 10: Projeção estereográfica
Por último, também conseguimos encontrar a espiral de Arquimedes nas galáxias, as Galáxias Espirais:
A característica mais marcante destas galáxias são seus braços espirais, evidentemente, onde ocorre intensa formação estrelar. As galáxias espirais, apresentam ainda um bojo no centro do disco, cuja importância relativa diminui conforme o tipo morfológico seja mais tardio; e um halo de material estelar, constituído basicamente de aglomerados estrelares e estrelas pobres em metais; além do halo de matéria escura. A dimensão radial dos discos é tipicamente de ordem de kiloparsecs, enquanto que a escala de altura é de poucas centenas de parsecs (MACHADO, 2006).
Figura 11: Galáxias Espirais

Em suma, a espiral de Arquimedes é uma das curvas com mais aplicações no cotidiano, podendo facilmente ser encontrada na natureza, como também em criações humanas. Outros exemplos são a espiral de Fermat e logarítmica, espiral de Littus e Parker. Consoante a isso, talvez o leitor possa concordar com o que o Peter Parker diz ao Doutor Estranho: “Sabe o que mais legal que magia? Matemática.”
REFERÊNCIAS
ALMEIDA, M. F. S.; CAVALHEIRO, G. L.; PAIVA, L. R. M.; ANDRADE, A. O.; PEREIRA,A. A.: Estudo do tremor cinético através da análise de desenhos manuais. Disponível em: https://www.peteletricaufu.com.br/static/ceel/doc/artigos/artigos2010/ceel2010_76.pdf. Acesso em: 28 fev. 2022.
Archimedes. The Works of Archimedes. Dover, New York, 2002. Translated and edited in modern notation by T. L. Heath.
FRANCO, Bernadette Dora Gombossy de Melo. Métodos Rápidos de Análise Microbiológica de Alimentos: Estudo Critico e Avaliação de Novas Metodologias. Tese de Doutorado. Universidade de São Paulo, 1994.
GOMES, A. R. Análise Comparativa de mecanismos de compressão para aplicação em refrigeração doméstica. Dissertação de Mestrado. Universidade Federal de Santa Catarina Florianópolis, 2006.
MACHADO, R. E. G.: Halos Triaxiais e a razão axial de galáxias espirais. Dissertação apresentada ao Departamento de Astronomia, Geofísica e ciências Atmosféricas para obtenção do título de Mestre em Astronomia. Universidade de São Paulo, 2006.
RESENDE, Kepler Alves: Curvas e Aplicações. Dissertação de Mestrado. Universidade Federal de Goiás, 2017.
SILVA, Felipe Olavo: Espiral logarítmica: da natureza para a sala de aula. Trabalho de Conclusão de Curso. Universidade Federal do Estado do Rio de Janeiro, 2015
VELOSO, Eduardo. Uma Curva de Cada Vez… A Espiral de Arquimedes. In: Revista
Educação e Matemática. Disponivel em: https://em.apm.pt/index.php/em/article/view/2401.
Acesso em: 28 fev. 2022.