Pedro Vítor dos Santos Barbosa − Matemática, UFCG
pedrovt91@gmail.com
Programa de Educação Tutorial (PET) – Matemática e Estatística
Ao iniciar esse texto eu gostaria de fazer a seguinte afirmação: “eu estou mentindo”. Mas e agora, será que eu estou mesmo mentido? Caso eu esteja, então eu falei a verdade e não estou mentindo, mas caso eu não esteja então eu estaria mentindo sobre estar mentindo. Confuso, não? Toda essa confusão não tem uma resposta certa, mas nos ajuda a entender um conceito mais simples e muito importante: o conceito de paradoxo.
Um paradoxo é um caso ou proposição que contraria os conceitos da lógica ou que gera uma aparente falta de nexo. De forma mais ampla, é algo que logicamente não faz sentido, pelo menos não em uma primeira abordagem.
É nesse contexto que irei apresentar alguns casos de paradoxos envolvendo cálculos probabilísticos que podem mexer com sua cabeça. Você pode tentar resolver a problemática de cada situação antes de ler sobre a resolução.
Paradoxo dos dados
Jogando com três dados, 9 e 10 pontos podem ser obtidos de seis maneiras diferentes:
Tabela 1: combinações possíveis para 9 e 10 pontos.
| 9 pontos | 10 pontos |
| 1, 2, 6 | 1, 3, 6 |
| 1, 3, 5 | 1, 4, 5 |
| 1, 4, 4 | 2, 2, 6 |
| 2, 2, 5 | 2, 3, 5 |
| 2, 3, 4 | 2, 4, 4 |
| 3, 3, 3 | 3, 3, 4 |
O esperado pela maioria das pessoas é que, ao jogar três dados simultaneamente, a frequência com que a soma resulta em 9 ou 10 seja igual ou muito parecida. Entretanto, observasse que a soma resulta em 10 pontos com uma frequência consideravelmente maior que resulta em 9 pontos. Por que isso acontece?
Esse problema chegou a ser estudado por grandes matemáticos dos séculos XVI e XVII como Girolamo Cardano e Galileu Galilei.
A resposta para essa pergunta pode não soar óbvia se nos deixarmos levar pela narrativa do problema, mas é importante lembrar que as possibilidades de cada uma das combinações dos dados não são necessariamente iguais, então nos resta mostrar que os dados de fato têm uma maior chance de somarem 10 pontos quando comparados aos 9 pontos.
Note que, por exemplo, a chance de os dados resultarem em (6, 3, 1) é maior do que (3, 3, 3), já que a ordem dos dados não importa o primeiro tem 3! = 6 possibilidades de acontecer, enquanto o segundo tem apenas uma. Dessa forma, podemos analisar cada um dos casos.
Tabela 2: possibilidades de cada combinação para 9 e 10 pontos
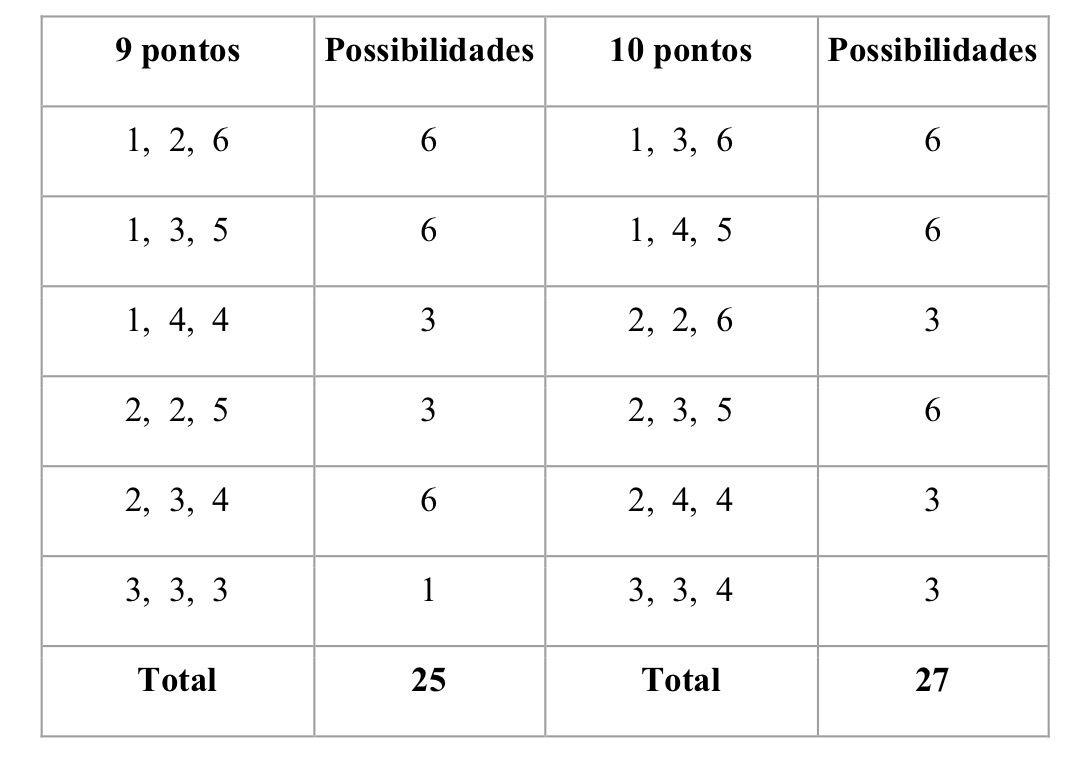
Analisando a tabela acima, vemos que na verdade a probabilidade de obtermos 10 pontos é de fato maior que obtermos 9 pontos, e assim desvendamos nosso primeiro paradoxo. A verdade é que os dados podem enganar as vezes, mas a matemática é sempre verdadeira
Paradoxo da divisão
O nosso segundo paradoxo provém da análise de uma situação hipotética:
“Dois jogadores jogam uma série de partidas justas até que um deles obtenha 6 vitórias. Por motivos exteriores ao jogo, este é interrompido quando um dos jogadores somava 5 vitórias e o outro 3 vitórias. Como devemos dividir, de forma justa, o montante apostado por ambos os jogadores?”
Em 1494, o matemático Luca Pacioli sugeriu a seguinte maneira de resolver o problema: Como haviam ocorrido 8 partidas, o prêmio deveria ser dividido com mesma proporção às vitórias de cada jogador. Ou seja, como foram disputadas 8 partidas com 5 vitórias de um jogador e três do outro, 5/8 do prêmio deveriam ficar com o primeiro jogador e 3/8 com o outro, o que resolveria o problema… ou será que não?
Assim como o problema anterior, esse problema foi tema de discussão de grandes matemáticos que apontavam falhas na solução apresentada por Pacioli. No século XVI Nicolo Tartaglia e Girolamo Cardano já diziam não se tratar de uma divisão justa e conter um erro evidente. Já no século XVII, Pascal e Fermat trocaram uma correspondência onde nela apresentavam uma solução probabilística para o problema.
Para a dupla, cada jogador deveria receber 𝑝 𝑥 𝑝𝑟ê𝑚𝑖𝑜 onde 𝑝 representaria a probabilidade de o jogador ganhar caso as partidas continuassem. Assim, vamos analisar os casos:
Figura 1: Todos os casos possíveis para o jogo
Perceba que o jogador A que havia vencido 5 jogos tem uma probabilidade igual a 7/8 de vencer, enquanto o jogador B teria uma chance de 1/8, logo os prêmios deveriam ser proporcionais a esses números.
Paradoxo do dia do aniversário
Qual a chance de 2 pessoas fazerem aniversário no mesmo dia? Com menos de 365 pessoas não podemos garantir que isso ocorra. Mas quais são as chances de isso acontecer em grupos menores?
A noção comum para esse paradoxo é de que para grupos relativamente pequenos como 30 ou 40 pessoas essa chance seria pequena ou moderada, mas será que é mesmo? Vamos assumir um grupo de 𝑛 pessoas com 𝑛 < 365. É fácil perceber que a chance de duas pessoas não fazerem aniversário no mesmo dia é muito grande, já que uma vez definido o aniversário da primeira pessoa, a segunda poderia aniversariar em qualquer um dos outros 364 dias (assumindo anos que não sejam bissextos), ou seja, uma chance de $1 – \frac{1}{365}$. Essa lógica se estende para um número maior de pessoas. Assumindo que $\bar{P}(n)$ representa a chance de em um grupo com 𝑛 pessoas, duas nunca fazerem aniversário no mesmo dia, temos
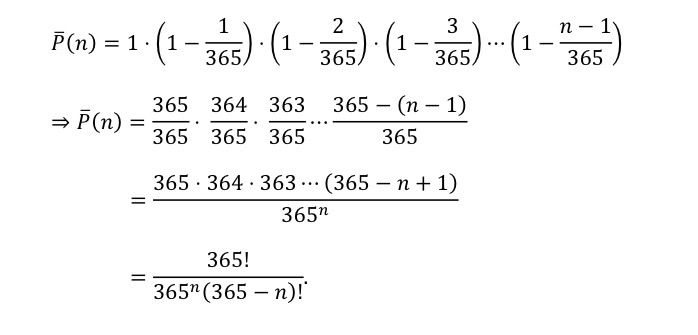
Assim, para acharmos a probabilidade 𝑃(𝑛) de ter dois aniversariantes no mesmo dia, basta fazermos 𝑃(𝑛) = 1 − 𝑃̅(𝑛). Daí, com o auxílio de uma calculadora podemos obter os seguintes resultados para alguns valores de 𝑛:
Tabela 3: Relação entre 𝑛 pessoas e chance 𝑃(𝑛).
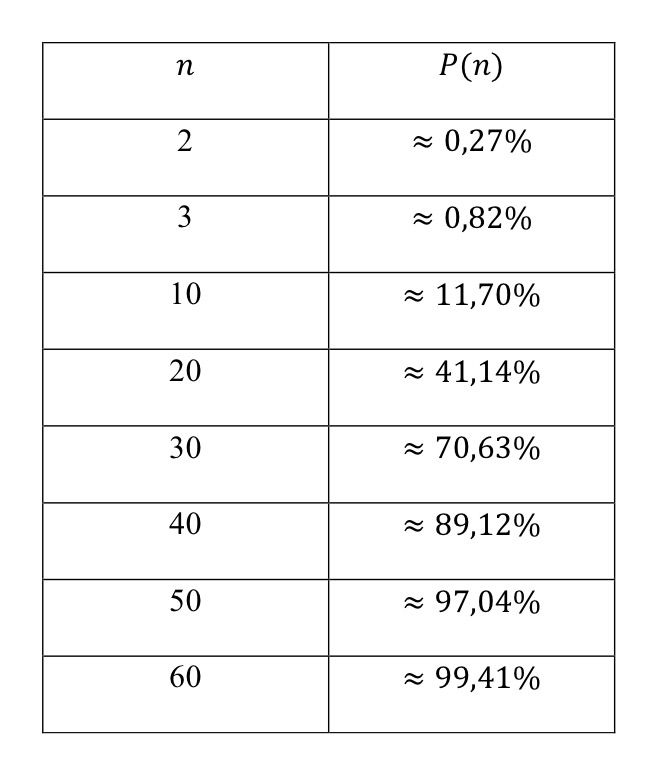
Ou seja, com um grupo pequeno de apenas 30 pessoas já temos uma probabilidade muito alta de 70% de duas dessas pessoas fazerem aniversário no mesmo dia, e bastam apenas 60 pessoas para essa probabilidade seja de 99%, contrariando o senso comum ao analisar brevemente essa questão.
Paradoxo das coincidências
Em uma festa de final de ano um grupo decide trazer presentes para um sorteio de amigo secreto, porém as pessoas trouxeram convidados que também vão participar. A questão é: quanto mais gente estiver participando do sorteio, mais difícil de tirar o próprio presente?
Em um primeiro momento parece que de fato a chance de retirar o próprio presente diminuirá, já que haverão muitos outros presentes, mas precisamos de algo que formalize essa situação para podermos fazer uma análise mais precisa.
Essa situação é um pouco diferente das que vimos até agora. Para calcular essa possibilidade usamos um recurso chamado de permutações caóticas ou desarranjo. Você pode ver melhor sobre isso em (1). Através dessa permutação podemos calcular que a probabilidade de retirar o próprio presente em um grupo de 𝑛 pessoas é descrita por:
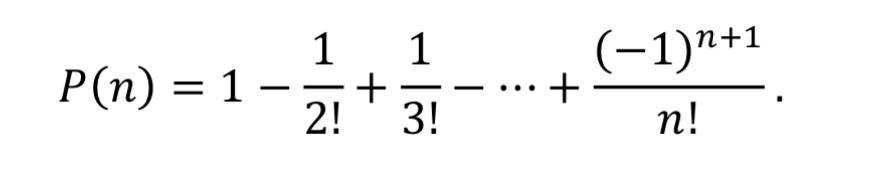
Com essa expressão podemos calcular essa probabilidade para alguns valores iniciais.
Tabela 4: Relação entre 𝑛 pessoas e chance de se sortear
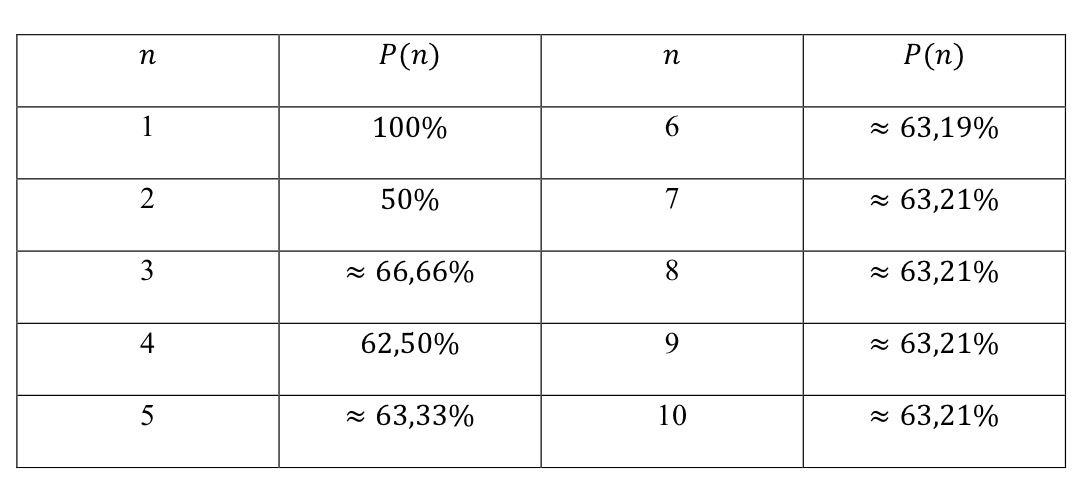
Como é possível ver, a probabilidade não chega a ter aumentos ou baixas significativas com o aumento de 𝑛, mas na verdade essa parece se estabilizar por volta dos 63,21%.
De fato, isso acontece, já que podemos aproximar a expressão de 𝑃(𝑛) através da série de Taylor aplicada à função exponencial obtendo
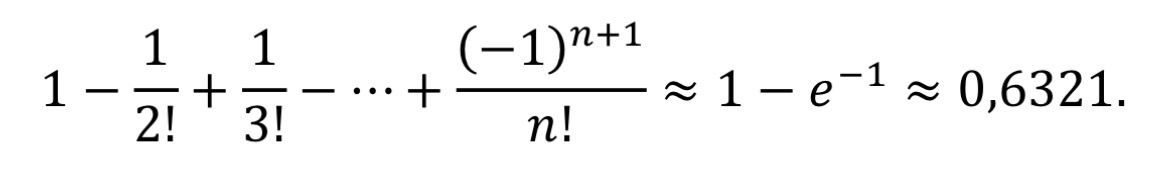
Portanto podemos ver que a probabilidade realmente se estabiliza, então não precisamos nos preocupar com o número de participantes em um sorteio de amigo secreto, já que isso não irá alterar significativamente a probabilidade de pessoas retirarem seus próprios presentes.
Esse paradoxo impressiona não por seu resultado, mas sim pela velocidade cm que os resultados se estabilizam, já que a partir de 4 participantes as variações já são menores que 1%.
REFERÊNCIAS
(1) VIANA, F.C.A. Estudo e Aplicações de Probabilidade Geométrica e Paradoxos, Dissertação de Mestrado, PROFMAT/SBM, Universidade Federal da Paraíba, João Pessoa, 2013.
(2) TENREIRO, C. Paradoxos Clássicos no Cálculo das Probabilidades, 2004. Disponível em: http://200.17.213.49/lib/exe/fetch.php/disciplinas:ce067:paradoxosclassicos.pdf