Ester Vanderlei Silva Avelino – Matemática, UFCG
ester.vanderlei@estudante.ufcg.edu.br
Programa de Educação Tutorial (PET) – Matemática e Estatística
Provavelmente, em algum momento da sua vida, você já se deparou com o infinito, seja ao contemplar as estrelas¹ ou ao tentar contar os grãos de areia na praia quando criança. Nesses momentos, é evidente a sensação de algo que parece não ter fim. Essa percepção também pode ser experimentada ao lidar com os números, pois não importa o quão grande seja o número que você pense, sempre é possível adicionar mais um, e encontrando um número maior ainda. Além disso, filósofos pioneiros também se depararam com essa questão, ao refletir sobre a vida após a morte ou a existência de um Deus Eterno².
Os números, por si só, podem transmitir a ideia fundamental do infinito: eles nunca terminam. No entanto, essa noção do infinito se revela de maneira distinta, seja na filosofia, na ciência, na matemática ou em outros domínios, assumindo diferentes formas como um número, um lugar, uma ideia ou um conceito. Cada área de estudo oferece perspectivas únicas sobre o infinito, explorando suas implicações e desafios de maneira singular.
O conceito de infinito tem sido constantemente objeto de questionamento, despertando interesse e debates entre matemáticos, filósofos, poetas³ , físicos e teólogos ao longo da história. Essas discussões não são recentes e remontam a civilizações antigas, segundo os estudos de Morris, o autor afirma que
“A história do Infinito, ou seja, a história do conceito de Infinito, não é somente uma história da Matemática; é antes uma história da evolução do pensamento científico e de como é possível se pensar em algo que transcende qualquer possibilidade de compreensão.”(1)
De maneira breve, vamos comentar um pouco sobre a definição do conceito de infinito nas diferentes áreas do conhecimento.
Conceitos dos infinitos
Na filosofia, encontramos várias maneiras de definir o infinito. Um primeiro sentido remete ao quantitativo, e possui uma conexão natural com a matemática em certos casos. Inicialmente, Aristóteles admitiu a possibilidade de se descrever o infinito de dois modos, em ato e em processo. Nesse contexto, há a menção do infinito potencial⁴ , que se refere a algo que pode se tornar infinito, ou seja, algo indefinido ou infinitamente grande, assim, considera que uma sucessão pode ser aumentada diversas vezes por adições ou multiplicações sucessivas, ou diminuída quantas vezes possa por divisões sucessivas. Por outro lado, temos o infinito atual⁵ , que representa algo atualmente maior do que qualquer quantidade dada da mesma natureza. (3)
Na matemática, o infinito potencial se refere a um processo no qual um número cresce além dos limites finitos, enquanto o infinito atual não é um processo, mas um número em si. Segundo Cantor, qualquer número finito pode ser visto como um processo infinito com uma espécie de evolução (infinito potencial), ou como uma constante fixa que representa o processo completo (infinito em ato).
De acordo com Cantor, o infinito é um limite inalcançável, uma sequência infinita de números. Por exemplo, os números 1, 2, 3, 4, 5, … podem continuar indefinidamente, mas nunca chegarão ao último número no infinito. Sob essa perspectiva, cada número na sequência é apenas um passo em um processo infinito. No entanto, o limite nunca alcançado pode ser visto como um número em si, denominado número transfinito. Para Cantor, esse número transfinito é considerado uma “quantidade, fixa, constante, para além de todas as quantidades finitas”.(2)
Os Limites do Infinito
Na física, o infinito é abordado em várias perspectivas. Por exemplo, no contexto do espaço e do tempo, algumas teorias consideram a possibilidade de um universo infinito, onde não há limites ou fronteiras definidas. Entretanto, com o desenvolvimento da Teoria da Relatividade Geral e da mecânica quântica de Einstein, essa concepção tem sido questionada e reconsiderada.
Apesar da teoria do universo infinito estar sendo descartada, a física apresenta teorias de onde poderíamos encontrar infinitos reais. Na física quântica, surgem conceitos de infinitos matemáticos e singularidades em certos fenômenos, como as equações de campo de partículas elementares ou buracos negros.
Os buracos negros são objetos massivos nos quais toda a matéria é comprimida de forma extremamente densa, criando uma região chamada horizonte de eventos. Segundo a teoria de Einstein da relatividade geral diz que uma vez que você cruza o horizonte de eventos, você vai continuar caindo em direção à singularidade.

Fonte: https://super.abril.com.br/ciencia/nasa-divulga-primeira-imagem-de-um-buraco-negro
A singularidade é uma região de densidade e curvatura do espaço-tempo infinitas, onde as leis da física tal como as conhecemos deixam de ser aplicáveis. A teoria diz que ao ultrapassar o horizonte de eventos de um buraco negro, você seria atraído em direção à singularidade e, em questão de microssegundos, chegaria a esta região de curvatura e densidade infinita e simplesmente deixaria de existir. Por isso, nessa região, as leis da física que conhecemos deixam de ser aplicáveis, pois as propriedades do espaço-tempo tornam-se extremas.(4)
Um recorte histórico do conceito de Infinito na Matemática
Os matemáticos precisavam encontrar uma maneira de lidar com o infinito. Era necessário encontrar uma forma de compreender e estudar algo completamente estranho e não intuitivo. No entanto, dominar o infinito e torná-lo observável exigiu a colaboração de diversos matemáticos, filósofos e cientistas.
Os gregos foram os primeiros a se deparar com o conceito do infinito na matemática. Os Pitagóricos ao tentarem calcular a medida da diagonal de um quadrado de lado 1, descobriram que a raiz quadrada de 2 era um número irracional, com infinitas casas decimais. Também encontraram desafios matemáticos envolvendo segmentos de reta e curvas chamados de incomensuráveis, como o comprimento da circunferência com diâmetro igual a 1, que conhecemos como 𝜋. (2)
Nesse mesmo período, temos o filósofo e matemático grego Zenão de Eleia, que apresentou alguns argumentos⁶ para tentar provar a inconsistência dos conceitos de multiplicidade e de divisibilidade, criando a partir daí quatro paradoxos que exploravam a divisibilidade infinita do espaço e do tempo, que mais tarde levariam ao desenvolvimento do cálculo.
Um dos paradoxos mais conhecidos de Zenão é o paradoxo de Aquiles e a tartaruga. Nessa história hipotética, Aquiles, um herói grego de alta velocidade, desafia uma tartaruga para uma corrida. No entanto, para nivelar a disputa, a tartaruga recebe uma vantagem inicial, começando alguns metros à frente da linha de partida de Aquiles. Zenão argumenta que, independentemente do tempo decorrido na corrida, Aquiles nunca conseguirá ultrapassar a tartaruga (3). Por exemplo, se a tartaruga fosse duas vezes mais lenta que Aquiles e Aquiles desse uma vantagem de um quarteirão a ela: quando Aquiles percorrer o mesmo quarteirão a tartaruga andou metade do outro, Aquiles anda meio quarteirão e a tartaruga anda a metade deste, ou seja, um quarto, e assim infinitamente. A vantagem vai reduzindo gradativamente, mas sempre tem uma mínima diferença entre eles.
Esse paradoxo intrigou os gregos e foi motivo de discursão entre eles, pois, eles sabiam que numa disputa real, Aquiles venceria a tartaruga sem problemas. Além disso, que essa corrida representa uma soma infinita, onde cada parcela é a distância percorrida por Aquiles a cada instante, começando com um quarteirão, depois meio quarteirão e assim por diante, ou seja, ficaria assim:
$1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots$
e, embora essa soma parecesse impossível na época, os gregos sabiam que ela resulta em 2. Ou seja, Aquiles ultrapassaria a tartaruga no segundo quarteirão. (2)
No século 4 e 3 a.C., Eudoxo de Cnido e Arquimedes utilizando o método da exaustão para calcular áreas limitadas por curvas e contribuíram para o desenvolvimento do conceito de limite. De maneira simples, método da exaustão consiste em colocar figuras dentro de figuras. A figura abaixo, ilustra esse método da forma como conhecemos nos cursos de Cálculo I.
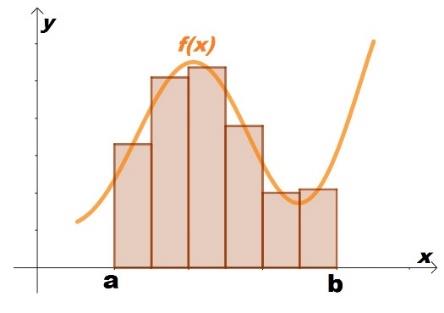
Fonte: https://www.dicasdecalculo.com.br/conteudos/integrais/
No século XVII, temos Isaac Newton e Gottfried Leibniz desenvolvendo cálculo infinitesimal, tendo o método da exaustão um grande catalizador, e, daí, surgiram fórmulas para o cálculo das mais variadas áreas e volumes. No entanto, eles não foram capazes de definir precisamente o que eram as quantidades infinitamente pequenas. E foi só cerca de um século depois, que Augustin-Louis Cauchy substituiu o conceito de infinitésimo pela ideia de limite.
Augustin Louis Cauchy criou o conceito de limite como forma de dar sentido a sequências infinitas. Ele argumentava que a soma 1 + 1/2 + 1/4 + … não era igual a 2, mas que tendia a 2 sem nunca o alcançar.
No século XIX, temos a ilustre figura de Georg Cantor que trouxe uma grande contribuição para matemática ao definir e estabelecer propriedades sobre o infinito atual⁷ . Ele fez isso ao questionou se todos os números racionais preencheriam todos os pontos de uma reta de forma correspondente, e teve a ideia de “contar” os números inteiros, “contar” os números racionais, e todos os números reais⁸ .
Ao fazer isso, Cantor descobriu que os números racionais têm a mesma cardinalidade que os números inteiros. E ao tentar emparelhar os números inteiros com os números reais, ele primeiro comparou com os algébricos⁹ , provando que têm a mesma cardinalidade. Entretanto, ao comparar os números reais com os números inteiros e descobriu que os reais têm uma cardinalidade maior.
Em síntese, Cantor mostrou, em relação ao tamanho dos conjuntos, que há infinitos iguais e diferentes¹⁰ .
¹ “O céu, que é perfeito, andou jogando em seus olhos o dom do infinito.” (Humberto del Maestro)
² “Pelo nome de Deus entendo uma substância infinita, eterna, imutável, independente, onisciente, onipotente, e pela qual, eu-mesmo, e todas as outras coisas que são (…) foram criadas e produzidas.” (René Descartes)
³ “Que não seja imortal, posto que é chama. Mas que seja infinito enquanto dure.” (Vinicius de Moraes)
⁴ “Quod actu quidem finitum est, sed augeri sine fine potest”
⁵ “Infinitium actuale quod actu habet esse sine limite.”
⁶ “Zenão, objetivando mostrar aos matemáticos da época as incoerências decorrentes da tentativa de se completar grandezas contínuas com um número infinito de pequenas partículas, apresentou alguns paradoxos” (Lorin & Nogueira,2015, p. 124)
⁷ Até então o infinito era tratado pela concepção aristotélica do infinito em potencial, ou seja, uma ideia de infinito que não tem fim, limite nem existência física.
⁸ É claro que Cantor não estava interessado em saber exatamente quantos números existem, mas sim descobrir se dava para estabelecer uma relação entre dois ou mais destes conjuntos.
⁹ Os números algébricos são os números que podem ser raízes de uma equação algébrica. Por exemplo, o número 𝜋 não pode ser uma raiz de uma equação algébrica, pois esse número surge através de processos infinitos de análise.
¹⁰ “Alguns infinitos são maiores que outros.” (John Green)
REFERÊNCIAS
(1) MORRIS, R. Uma Breve História do Infinito: Dos Paradoxos de Zenão ao Universo Quântico. Jorge Zahar Editor. Rio de Janeiro. 2003.
(2) SANTOS, Tatiana de Souza Lima. O conceito de infinito: uma abordagem a partir da resolução de problema. Orientador: Prof. Dr. Evandro Carlos Ferreira dos Santos. 2015. Dissertação (Mestrado) – Matemática, PROFMAT, UFBA Salvador – Bahia, 2015.
(3) SIQUEIRA, Fernanda Kelly da Silva. LORIN, João Henrique. Os conceitos de infinito atual e
(4) UMA VIAGEM AO INFINITO. A Trip to Infinity. Direção: Drew Takahashi Jonathan Halperin. Netflix, 2022
